数到头,脑袋疼:数学奇谜录

在数学的世界里,有一些问题看似简单,但却蕴含着深刻的智慧和挑战。这些问题,不仅能让人笑一笑,还能让人头大如斗。这篇文章将带你走进一个充满趣味与挑战的数学奇谜之旅,让我们一起探索那些有趣又烧脑的数学题。
第一道难题:悖论中的悄然
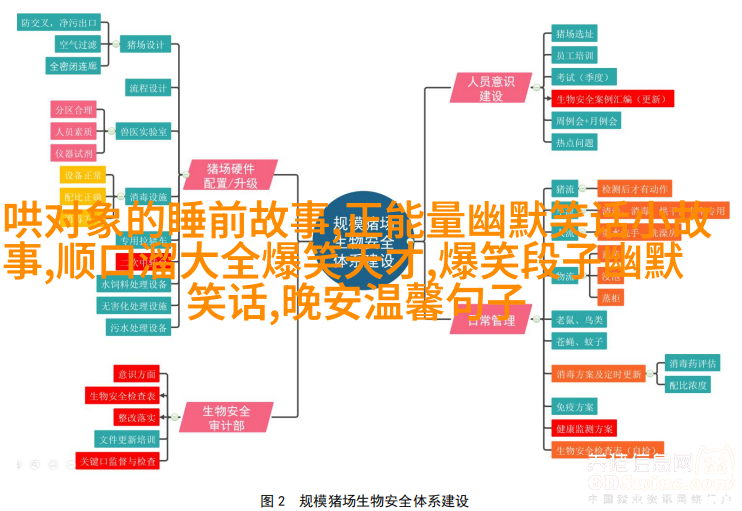
数学中的死胡同——柯尔定理
柯尔定理是由美国数学家罗伯特·柯尔提出的,它描述了一个看似无解的问题。这个定理表明,如果一个人站在原地一直跑,他最终会回到起点。但如果他每次跑步时都转个180度,那么他永远不会回到起点。这听起来有点像时间旅行者的困境,但实际上,这只是一个关于空间和角度运动的一个有趣悖论。
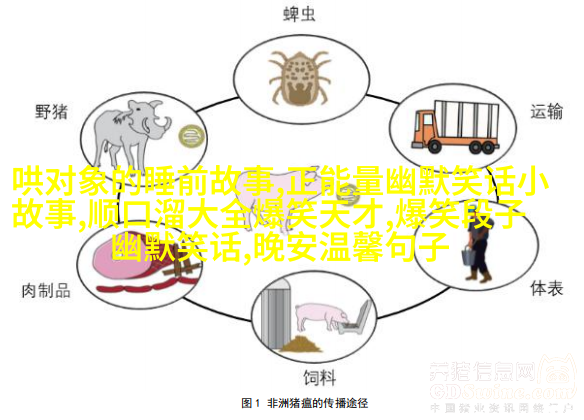
第二道难题:迷宫中的智者
转圈圈,找回路——莫拉斯环形木板问题

莫拉斯环形木板是一个著名的问题,它描述了这样一种情况:有一块圆盘,上面画着多个连续且不重叠的小方格,每个小方格中再画一个更小的圆盘,并重复此过程直至最后只剩下中心的小圆盘。当这块木板被旋转一定角度后,将其放回原位,我们需要找到旋转多少角度才能使所有的小方格重新排列成原始状态。这个问题虽然听起来简单,却要求解决者拥有高超的逻辑推理能力和对几何变化规律敏锐洞察力。
第三道难题:时间的大师

时间倒流,思维不倒——逆向计数谜团
想象一下,你被给予了一串数字,每个数字代表从100开始递减到的某一天。你必须通过逆向计算来找出每天对应哪些数字。在这个游戏中,每一天可能都会出现多种可能性,因为没有任何线索可以帮助你确定正确答案。而要做到这一点,就需要运用巧妙的手法,比如利用概率分析、逻辑推断甚至心理学知识来猜测那串神秘代码背后的规律。
第四道难题:空间大师
空间错综,视觉迷惑——三棱镜实验室之谜
在三棱镜实验室里,有三个房间,其中两个房间分别装饰成了不同的主题,而第三个房间则是一片空白。不过,这三个房间之间存在一种特殊关系,当你进入其中任意一个,都可以看到另外两个房间的一部分。如果你知道进入哪个房间,可以通过观察它所显示出来的内容来确定其他两个房里的装饰是什么样子的。但是,如果你不知道从哪里开始,你可能会陷入无尽循环,从而无法发现答案。这就是为什么有些人称这种情景为“信息过载”,因为它既考验你的直觉,也考验你的逻辑判断力。
第五道难题:抽象艺术家
抽象概念化,创造新世界——弗雷德曼图形怪异现象
弗雷德曼图形是一种特殊类型的地图,它能够展现出两地之间所有可行航线。在这个抽象概念化的情境下,我们可以构建出各种各样的路径网络,从而发现新的连接方式或隐藏规律。不仅如此,这类图形还常常用于社会学研究、城市规划等领域,为决策提供新的视角和工具,无疑也是极具挑战性的思考练习之一。
总结:
《数到头,脑袋疼》这篇文章带领读者穿越了五项不同风格但同样具有挑战性的数学任务,从哲学性质上的悖论,再到物理层面的空间变换,最终抵达艺术性质上的抽象呈现。每一项任务都需要读者运用不同的思维模式去理解并解决,使得整个阅读体验既愉快又富有教育意义。此外,由于这些任务涉及的是基本的人类认知能力,所以它们也反映出了人类如何通过创造性思维去适应不断变化的人生环境。
标签: 顺口溜大全爆笑天才 、 正能量幽默笑话小故事 、 爆笑段子幽默笑话 、 哄对象的睡前故事 、 晚安温馨句子



